Activité A (not so) gentle introduction to Excel

Consigne

Durant les 135 prochaines minutes, votre tâche est de réaliser une série de petites feuilles de calcul avec Excel dans le but d’en apprendre les bases.

Une suite bureautique est généralement composée d’un logiciel de traitement de texte (ou texteur), d’un logiciel de présentation et d’un tableur. Vous connaissez déjà les logiciels de traitement de texte (LibreOffice Writer, Google Doc ou Microsoft Word) et les logiciels de présentation (LibreOffice Impress, Google Slides ou Microsoft PowerPoint) pour les avoir utilisés ou étudiés dans le cadre de différents modules.

Quant aux tableurs, vous connaissez probablement l’emblématique Excel que l’on peut utiliser, par exemple, pour gérer son budget ou pour planifier une activité en réalisant un calendrier ou un diagramme de Gantt. Excel est le tableur de la suite de Microsoft, Calc est celui de LibreOffice et Sheets est celui de Google.

Avant d’aller plus avant et découvrir ce qu’est un tableur, voici ce qu’il n’est certainement pas :

• Un tableur n’est pas un logiciel de gestion de base de données. Même s’il est courant de voir de petites bases de données gérées à l’aide d’un tableur, cela revient à enfoncer des vis avec un marteau, cela peut fonctionner, mais ce n’est certainement pas la bonne façon de faire.
• Un tableur n’est pas un logiciel de traitement de texte. Là encore, s’il est sans aucun doute possible de produire une lettre avec un tableur, ce n’est, encore une fois, pas le bon outil.
• Un tableur n’est pas un logiciel de dessin à moins qu’il ne s’agisse d’une démarche artistique qui n’a alors pas sa place dans le cadre de l’activité professionnelle d’un informaticien.

D’une manière générale, on ne doit pas utiliser un tableur dans les cas où un logiciel plus adapté est disponible. Le fait qu’il soit nécessaire de préciser cela montre l’extrême polyvalence des tableurs. En effet, il y a bien peu de tâches en bureautique et en informatique qui ne peuvent être réalisées avec un tableur. Plus encore, presque tous les tableurs disponibles sont Turing complet et permettent donc, théoriquement, de réaliser n’importe quel algorithme.

Durant cette activité, vous allez découvrir que pour de petites applications, un tableur peut être une alternative pratique à un langage de programmation.

Objectifs

À la fin de ce travail, vous devez :

1. connaître et distinguer les notions de tableur et de feuille de calcul ;
2. connaître les notions d’expression ;
3. être capable de dire ce que peut contenir une cellule d’une feuille de calcul ;
4. être capable d’expliquer comment les cellules sont identifiées ;
5. être capable d’écrire une expression simple avec des références à d’autres cellules ;
6. être capable d’expliquer comment est évaluée une feuille de calcul ;
7. être capable d’utiliser la fonction SI (IF).

Ressources

Logiciel :

• Microsoft Excel

Première feuille de calcul et première formule

Pour commencer, nous allons une fois de plus réaliser l’algorithme d’Al-Khwârizmî pour résoudre une équation du deuxième degré de la forme :

Ouvrez Excel et créez un nouveau classeur vide (Nouveau classeur Excel) et enregistrez-le sous le nom programmes.xlsx. Dans Excel, un fichier .xlsx (ou .xls) est appelé « classeur » (workbook) et peut contenir une ou plusieurs feuilles de calcul (spreadsheet).

Lorsque le classeur est ouvert, double cliquez sur l’onglet « Feuil1 » qui se trouve en bas à gauche pour renommer la feuille et donnez-lui le nom QuadraticEquation1 comme sur la figure 2.

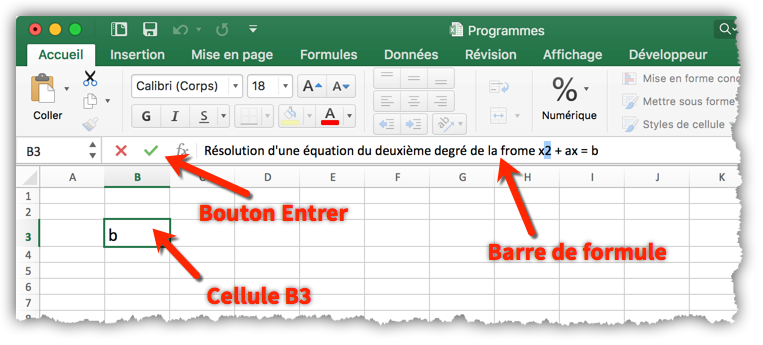
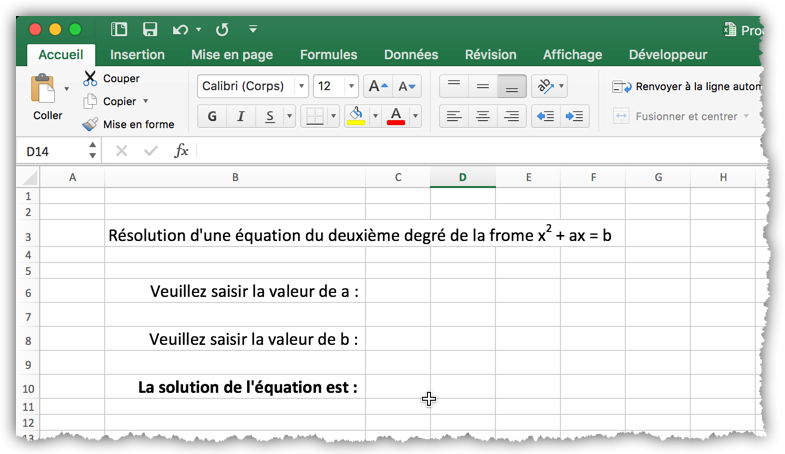
Sélectionnez maintenant la cellule B3 tapez le texte « Résolution d’une équation du deuxième degré de la forme x2 + ax = b » dans la barre de formule et cliquez sur le bouton « Entrer » pour terminer.

Pour éditer le contenu d’une cellule, sélectionnez la cellule et placez le curseur dans la barre de formule puis cliquez sur le bouton « Entrer » pour valider. Sélectionnez la cellule B3 et, dans la barre de formule, sélectionnez le 2 qui se trouve à côté du x et utilisez le menu contextuel « Format de cellule… » pour le mettre en exposant. Cliquez ensuite sur le bouton « Entrer » pour valider. Pour finir, assurez-vous que la cellule B3 est toujours sélectionnée et spécifiez une taille de 18 pt pour la fonte. Votre feuille de calcul devrait maintenant ressembler à celle de la figure 4.

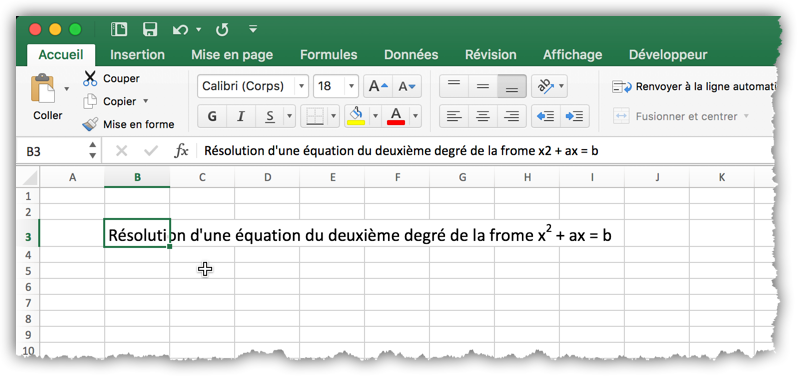
Le texte de la cellule B3 couvre les cellules B3 à I3, mais il s’agit bien du texte de la cellule B3. Si vous sélectionnez n’importe qu’elle autre cellule couverte par le texte, vous pouvez constater que la barre de formule est vide et si vous tapez une valeur dans l’une de ces cellules, vous pouvez constater que le texte de la cellule B3 est alors coupé; un texte ne couvre que des cellules vides.

Saisissez maintenant le texte « Veuillez saisir la valeur de a :  » dans la cellule B6, le texte « Veuillez saisir la valeur de b :  » dans la cellule B8 et le texte « Le résultat de l’équation est :  » dans la cellule B10. Sélectionnez ensuite les trois cellules en sélectionnant d’abord la première normalement puis les deux suivantes en maintenant la touche Ctrl enfoncée. Cliquez sur le bouton « Aligner à droite » pour aligner le texte à droite, spécifiez une taille de 18 pt pour la fonte et agrandissez la colonne B pour que le résultat ressemble à la figure 5. Pour finir, ajustez la taille et la graisse de la fonte des cellules C6, C8 et C10.

Nous savons déjà qu’une cellule peut contenir une valeur constante, c’est le cas des cellules dans lesquelles nous avons saisi un texte. En plus du type « texte » (chaîne de caractères), une valeur constante peut être de type « numérique », « booléen » (VRAI ou FAUX) ou encore « date ». Lorsqu’une cellule contient une valeur constante, le tableur détermine automatiquement son type. Une cellule peut aussi contenir ce qui est communément appelé une formule. En terme plus technique, une formule est une expression, c’est-à-dire une combinaison de littéraux (ou valeurs littérales), de variables, d’applications de fonction et d’opérations arithmétiques, logiques ou de comparaison. Pour indiquer au tableur que le texte que nous allons saisir est une expression qu’il doit évaluer, le premier caractère saisi doit être le signe égal =. Sélectionnez la cellule C10 et tapez le texte ci-dessous en veillant à ce que le signe égal soit le premier caractère.

= ((C6 / 2)^2 + C8)^0.5 - C6 / 2

Dans cette expression, C6et C8 sont des références aux cellules C6 et C8 dans lesquelles vous allez saisir les valeurs de a et de b. Les références aux cellules sont équivalentes aux variables des langages de programmation. L’accent circonflexe est l’opérateur d’élévation à la puissance. La puissance 0.5 (1/2) correspond à la racine carrée. Les autres opérateurs ont le même sens qu’en Java.

Lorsque l’on programme, on s’applique généralement à donner aux variables des noms qui ont une signification. Dans notre formule, on ne sait pas a priori à quoi correspondent les noms C6 et C8. Pour améliorer cela, il est possible de nommer les cellules qui ont un sens particulier.

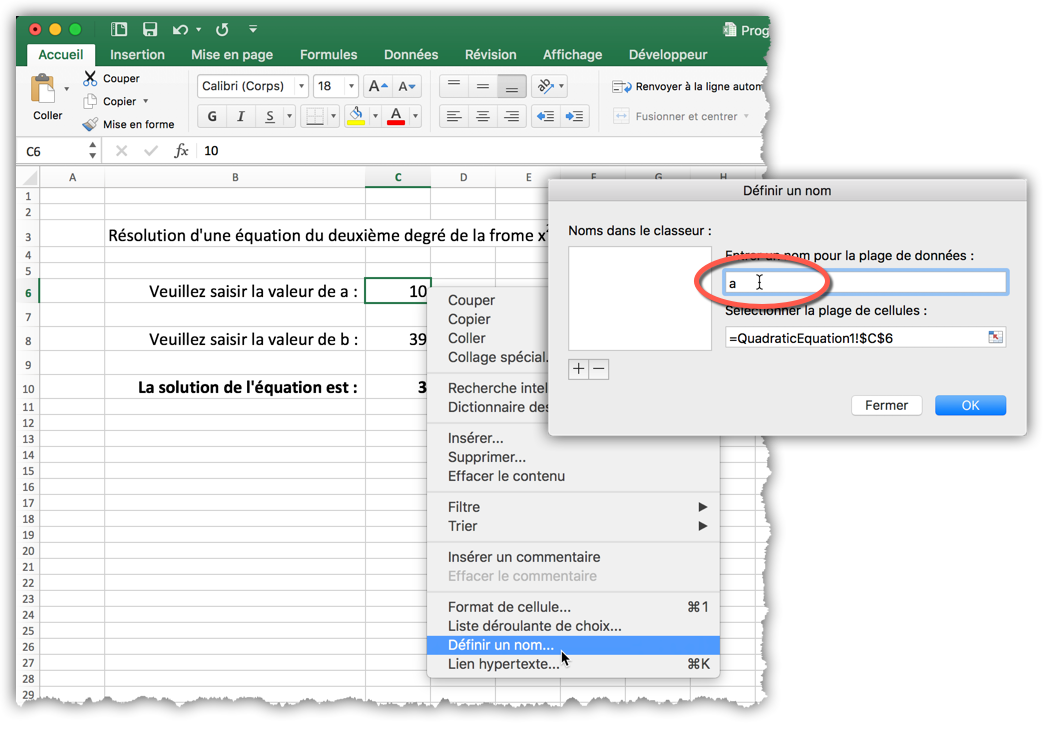
Sélectionnez la cellule C6 puis, dans le menu contextuel, cliquez « Définir un nom… ». Dans la boîte de dialogue qui s’ouvre, saisissez le nom « a » et cliquez OK. Faites de même avec C8 pour lui donner le nom « b ».

On peut maintenant réécrire l’expression de la cellule C10 d’une manière bien plus élégante et facile à lire :

= ((a / 2)^2 + b)^0.5 - a / 2

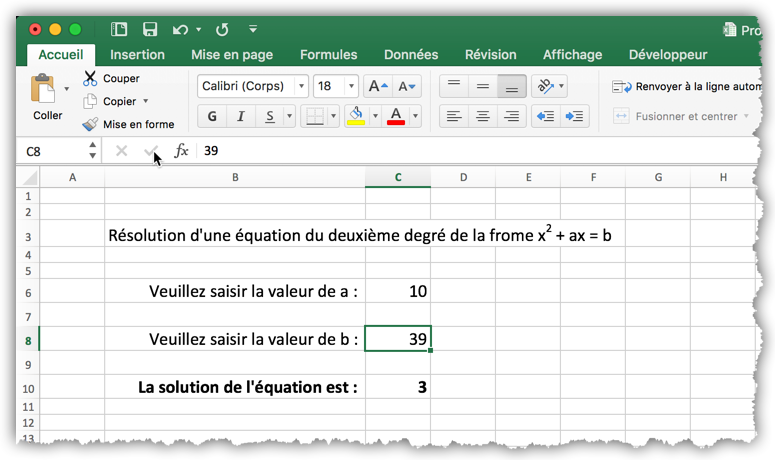
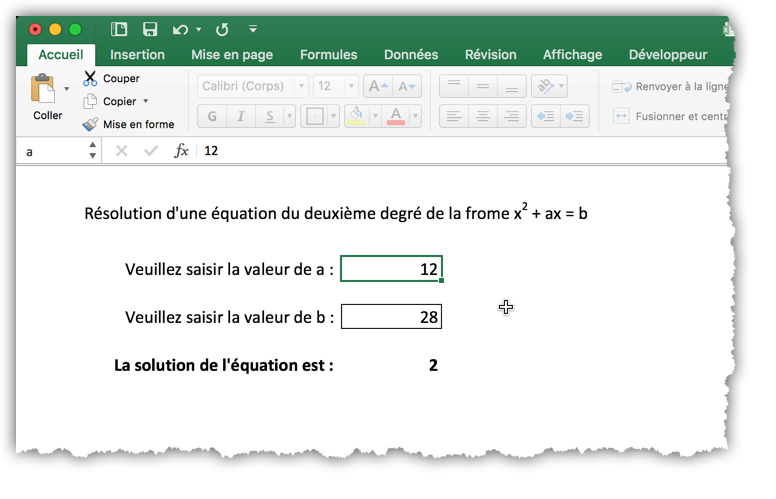
On peut tester le programme en saisissant la valeur 10 dans la cellule C6 et la valeur 39 dans la valeur C8. Si tout se passe bien, vous devriez lire la valeur 3 dans la cellule C10 comme le montre la figure 7. Vous pouvez observer que le tableur réévalue l’expression chaque fois que vous modifiez le contenu d’une cellule à l’aide de la barre de formule.

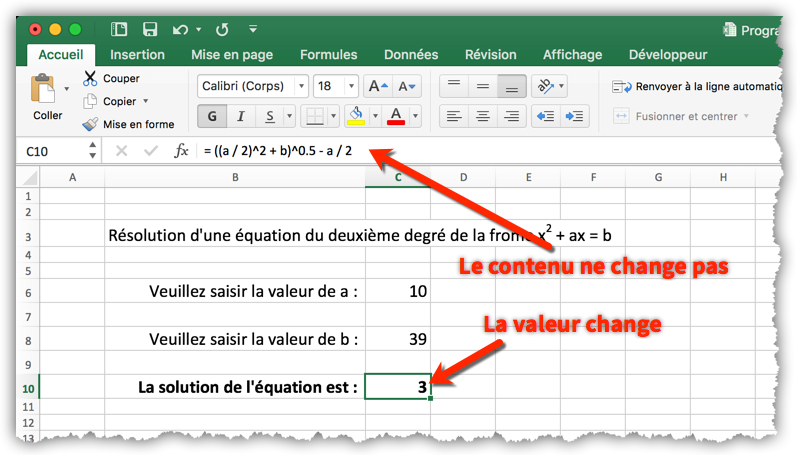
Important : la valeur affichée dans la cellule C10 n’est pas le contenu de cette cellule, mais l’évaluation de l’expression qu’elle contient. Le contenu de la cellule C10 est une expression (une formule) et non pas une valeur constante. Lorsque la valeur de C10 change parce que l’on a modifié le contenu de C6 ou de C8, le contenu de C10, lui, ne change pas comme le montre la figure 8.

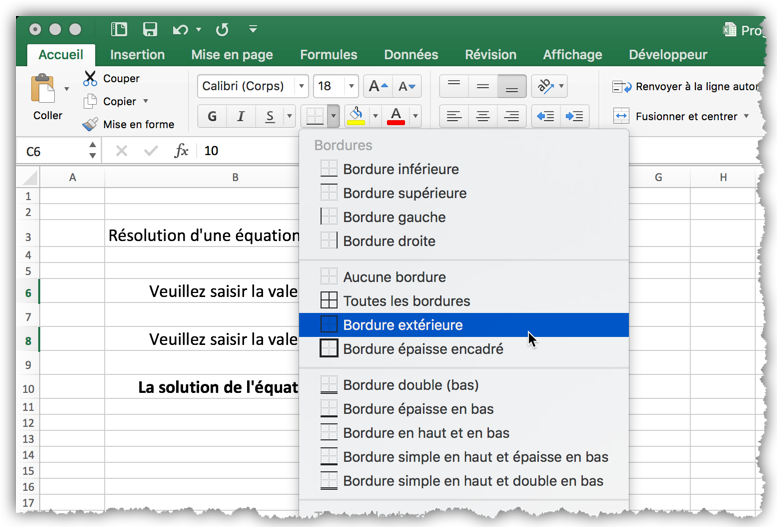
Pour rendre le programme (la feuille de calcul) plus facile à utiliser, on peut utiliser la protection des cellules pour empêcher la modification accidentelle du contenu des cellules autres que C6 et C8. Pour cela, sélectionnez la cellule C6 et, dans le menu contextuel, cliquez « Format de cellule… ». Dans la boîte de dialogue, rendez-vous sur l’onglet « Protection » et décochez l’option « Verrouillé ». Faites de même pour la cellule C8.

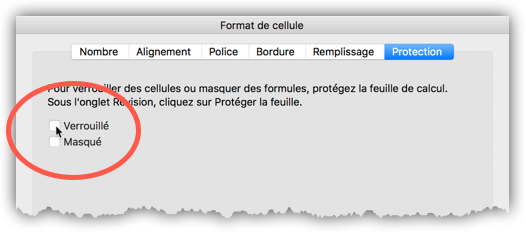
Pour mettre en évidence les cellules dans lesquelles l’utilisateur doit saisir une valeur, nous allons les entourer d’une bordure et cacher le quadrillage de la feuille. Sélectionnez les deux cellules C6 et C8, puis cliquez sur l’outil « bordure » et sélectionnez « Bordure extérieure ». Dans l’onglet « Affichage » du ruban, décochez les options « Entêtes » (Headings) et « Quadrillage » (Gridlines).

Enfin, pour activez la protection des cellules, sélectionnez « Protéger la feuille » dans l’onglet « Révision ». Votre feuille de calcul est maintenant terminée et devrait ressembler à celle de la figure 11.

Fonction conditionnelle

Si l’on peut, du moins en théorie, réaliser n’importe quel algorithme avec un tableur, on ne le fait pas de la même manière qu’avec un langage impératif comme Java. Un tableur n’a qu’une seule instruction et elle consiste à évaluer toutes les cellules. Cette unique instruction est exécutée à chaque fois qu’on modifie le contenu d’une cellule avec la barre de formule.

De fait, il n’y a pas de structures de choix pour sélectionner une séquence d’instructions ou une autre selon qu’une condition est remplie ou non ni de structures de boucle pour répéter une séquence d’instructions. Nous allons nous concentrer maintenant sur la question des choix. Le problème des boucles est abordé dans une prochaine activité.

Pour effectuer un choix dans un tableur, on utilise la fonction SI (IF). La fonction SI est une fonction qui prend trois paramètres : le premier est une expression booléenne (la condition), le second est la valeur à renvoyer si la condition est vraie, le troisième est la valeur à renvoyer si la condition est fausse.

Pour utiliser cette fonction, nous allons réaliser une feuille de calcul QuadraticEquation2 pour résoudre une équation du deuxième de degré de la forme :

Dans votre classeur, ajoutez une feuille de calcul et nommez-la QuadraticEquation2.

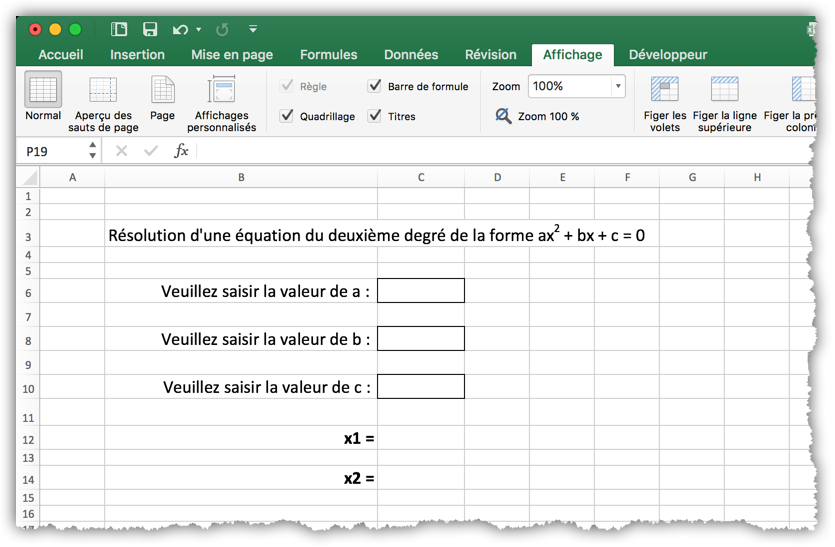
Utilisez les connaissances acquises jusqu’ici pour créer une feuille qui ressemble à la figure 13 et donnez aux cellules C6, C8 et C10, les noms suivants : a_, b_ et c_. La portée d’un nom est le classeur tout entier, de fait les noms a et b sont déjà utilisés. Ne vous occupez que de l’aspect visuel, il n’y a pas de formules à saisir pour l’instant.

Pour effectuer le calcul, on a besoin de connaître la valeur du paramètre ∆ (delta) qui se calcule comme suit :

Nous allons utiliser une cellule pour effectuer ce calcul, mais comme il n’intéresse pas l’utilisateur nous allons utiliser une cellule dans une zone que l’on pourra cacher par la suite. Sélectionnez la cellule K6 et saisissez le texte « delta : », puis sélectionnez la cellule L6, nommez-la « delta » et saisissez la formule suivante :

= b_^2 - 4 * a_ * c_

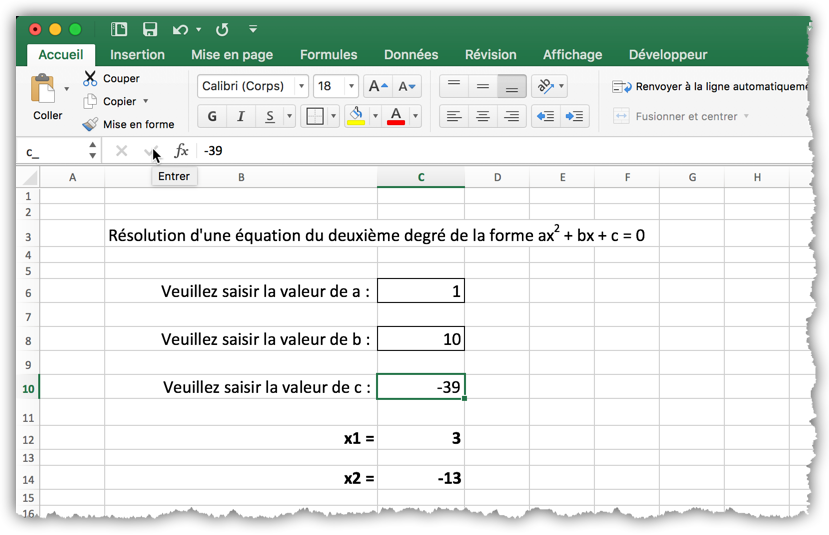
Si la valeur du paramètre ∆ est plus petite que zéro alors l’équation n’a pas de solutions réelles et l’on doit en informer l’utilisateur. En revanche, si le paramètre ∆ est plus grand que 0, alors on peut calculer la première solution (x1) avec la formule

= (-b_ + delta^0.5) / (2 * a_)

et la deuxième solution (x2) avec la formule

= (-b_ - delta^ 0.5) / (2 * a_)

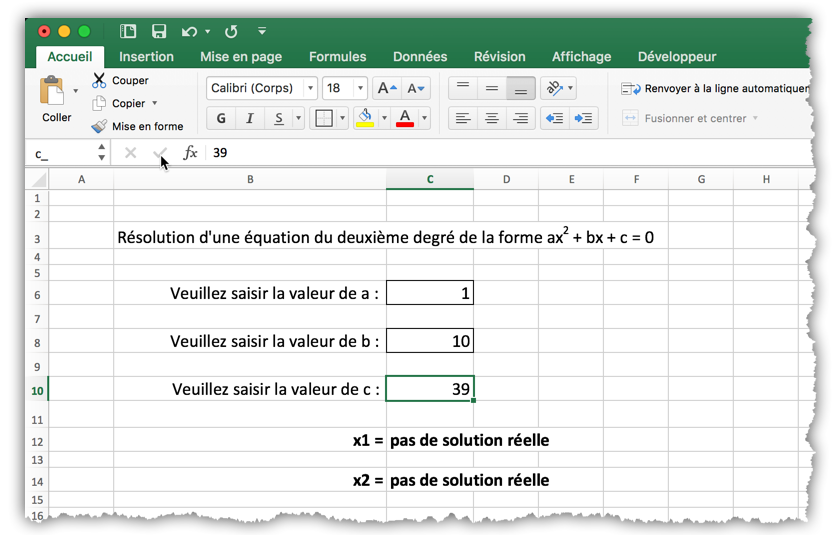
Mais comme on doit informer l’utilisateur qu’il n’y a pas de solution si le paramètre est inférieur à zéro, nous avons besoin de la fonction SI (IF). La formule de la cellule C12 devient :

= SI( delta < 0 ; "pas de solution réelle" ; (-b_ + delta^0.5) / (2 * a_))

La syntaxe de l’appel d’une fonction dans Excel ressemble beaucoup à celle de Java à ceci près que les paramètres sont séparés par des points-virgules (;) plutôt que par des virgules (,). Effectuez le même travail pour la cellule C14.

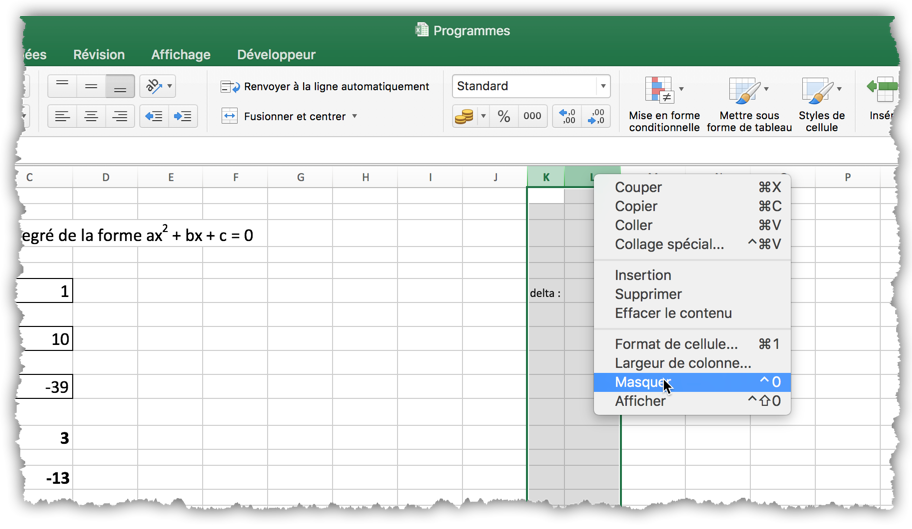
On peut maintenant cacher les colonnes qui contiennent le calcul du paramètre ∆. Pour cela, sélectionnez les deux colonnes puis, dans le menu contextuel, sélectionnez « Masquer ».

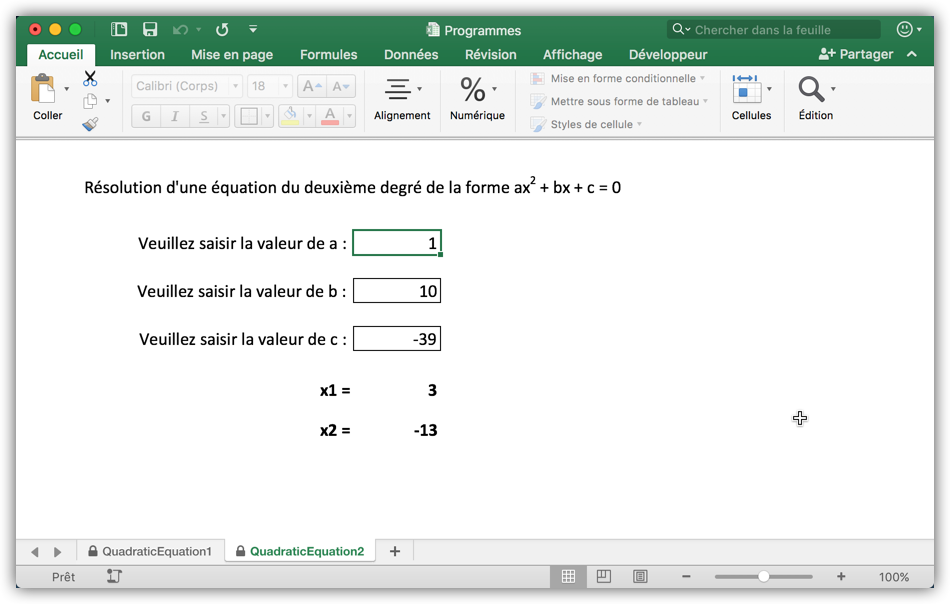
Rendez la feuille de calcul plus facile à utiliser en procédant comme pour la précédente. Le résultat final devrait ressembler à la figure 16.

Exercice

Modifiez la feuille de calcul de telle sorte que le texte « pas de solution réelle » ne soit pas écrit « en dur » une fois dans chaque formule, mais qu’il se trouve dans une cellule cachée à laquelle les deux formules font référence.

Pour cela, vous devez bien sûr ôter la protection de la feuille, afficher le quadrillage, les titres (en-tête des lignes et des colonnes), la barre de formule et trouver comment afficher à nouveau les colonnes masquées. Entraînez-vous à faire ces manipulations.